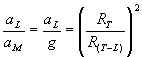Aceleração circular uniforme

Aaceleração circular uniforme, a que Newton dá o nome de centrípeta.

Newton propôs o que chamamos hoje de lei da gravitação de Newton; toda a partícula que atrai qualquer outra com uma força gravitacional.

Lei da gravitação para órbitas circulares:

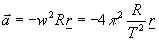
De acordo com a 2ª Lei de Newton, o movimento é uniforme para uma órbita circular. A aceleração neste caso é centrípeta, cuja velocidade angular é dada pela equação w = 2p /T em uma certa órbita circular de raio R. Onde r é o vetor unitário na direção radial.

Se m é a massa do planeta, então a força que atua sobre ele é dada pela 2ª Lei de Newton:

Pela 3ª lei de Kepler temos:

Onde C tem mesmo valor para todos os planetas. Então:

Baseando-se na lei dos períodos de Kepler, Newton concluiu que a força gravitacional varia inversamente com o quadrado da distância do planeta ao sol. Pela 3ª Lei de Newton , o planeta exerce uma força igual e contraria sobre o sol, a qual deve ser proporcional à massa M do sol. Newton, por sua vez, foi levado à expressão acima.

Onde G seria agora uma "constante universal" característica da força gravitacional. Esta é portanto, a lei de Newton da gravitação. A lei universal da gravitação de Newton, pode ser enunciada da seguinte forma:

"Cada partícula do universo atrai cada uma das outras partículas com força diretamente proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância que as separa. A direção desta força é a da linha que une as partículas".

    Newton procurou comparar a força necessária para manter a Lua em sua órbita com a força da gravidade na superfície da Terra.

   Adotando a seguinte notação: T=Terra; L=Lua; M=maçã de uma árvore.

    Portanto, os módulos das forças mencionadas serão:

     

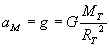
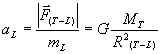
Sejam aL e aM os módulos das acelerações da Lua e da maçã; esta última é igual a g (gravidade). Além disso, R (T-M) =RT (raio da Terra).

Assim:

    Para fazer a verificação era necessário o valor de RT e R(T-L). Hiparco (130 a.C.) havia concluído que a distância da Terra à Lua é 59 vezes o raio da Terra através de seus cálculos. Newton usou o valor 60, obtendo assim:

O que concorda com o valor calculado da aceleração centrípeta da Lua.

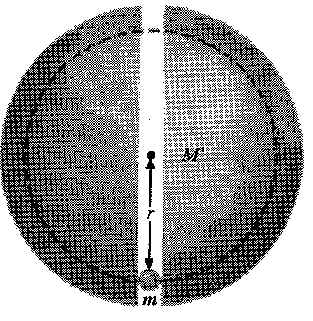
    Com isso, Newton deu uma contribuição básica à física mostrando que a força que mantém a Lua em sua órbita é a mesma que faz a maçã cair. Mas, para isso, Newton teve que considerar a Terra como uma casca esférica e com toda sua massa concentrada dentro do núcleo. Assim, do ponto de vista da maçã, a Terra se comporta como uma partícula, localizada no seu centro e tendo a sua massa (como mostra a figura a baixo).

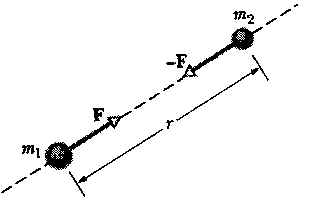
Newton não só concluiu que a Terra atrai a maçã e também a Lua, mas que qualquer corpo do universo atrai todos os outros (ver figura do lado direito). Duas maçãs, por exemplo, são atraídas uma pela outra a uma distância de 20 cm entre elas. Porém, há uma atração maior que é o das maçãs pela Terra, esta atração é tão grande que inibe os efeitos de atração entre as duas maçãs.

A maçã atrai a Terra com a mesma intensidade que a Terra atrai a maçã. Porém, suas acelerações são diferentes. A aceleração de uma maçã caindo é de 9,8 m/s2 (aceleração da gravidade da superfície da Terra). Já, uma bola de boliche de massa 7,0 kg sofre uma aceleração de 1,2x10-23 m/s2(como mostra a figura acima).