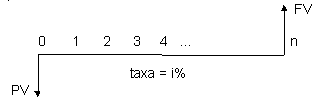Na fórmula S = P (1 + I) n , o principalP é também conhecido como Valor Presente
(PV = present value) e o montante S é também conhecido como Valor Futuro
(FV = future value).
Aliás, estas são as designações utilizadas na máquina HP12C.
A fórmula anterior pode então ser escrita:
FV = PV (1 + I) n e, como consequência, vem imediatamente que:
![]()
Isto pode ser representado graficamente através da figura abaixo, que representa um diagrama de fluxo de caixa , assunto que abordaremos mais detalhadamente na sequência do assunto.
Observe que FV no período n é equivalente a PV no período zero, se levarmos em conta a taxa de juros i. Esta interpretação é muito importante, como veremos no decorrer do curso. É conveniente registrar que existe a seguinte convenção: seta para cima, sinal positivo (dinheiro recebido) e seta para baixo, sinal negativo (dinheiro pago). Esta convenção é muito importante, inclusive quando se usa a calculadora HP 12C. Normalmente, ao entrar com o valor presente VP numa calculadora financeira, o fazemos seguindo esta convenção, mudando o sinal da quantia considerada como PV para negativo, usando a tecla CHS, que significa uma abreviação de "change signal", ou seja, "mudar o sinal". É conveniente ressaltar que se entrarmos com o PV positivo, a calculadora expressará o FV como um valor negativo e vice versa, já que as calculadoras financeiras, e aí inclui-se a HP 12C, foram projetadas, considerando esta convenção de sinais. Usaremos sempre a convenção de sinal negativo para VP e em consequência, sinal positivo para FV. Veremos com detalhes este aspecto, no desenvolvimento do curso.
Voltemos agora ao uso da calculadora HP12C
Apresentaremos a seguir a sequência de comandos na HP12C, para determinação de PV (valor presente), FV (valor futuro), i (taxa de juros) e n (número de períodos).
Cálculo de FV
- digite o valor presente PV
- tecle CHS
Nota: o CHS - abreviatura de change signal - muda o sinal para armazenar o valor de PV (present value) - dinheiro pago, conforme convenção.
- tecle PV
- digite 0
- tecle PMT
- digite a taxa i ( em %; ex.: i = 12% , digite 12)
- tecle i
- digite o número de períodos n
- tecle n
- tecle FV
Resposta no visor: o valor futuro procurado.
NOTA: Por enquanto, não se preocupe com a tecla PMT, que será explicada adiante. Basta saber que PMT é uma abreviação de payment , que significa pagamento, em inglês. O algarismo 0 (zero) digitado antes de teclar PMT, significa que você anulou o pagamento periódico PMT, uma vez que realmente êle não ocorreu.
Cálculo de PV
- entre com o valor de FV
- CHS ......FV
- 0
- PMT
- entre com o valor de n
- tecle n
- entre com o valor de i
- tecle i
- tecle PV
Cálculo de n
- entre com o valor de PV
- CHS ......PV
- 0
- PMT
- entre com o valor de FV
- tecle FV
- entre com o valor de i
- tecle i
- tecle n
Cálculo de i
- entre com o valor de PV
- CHS PV
- 0
- PMT
- entre com o valor de FV
- tecle FV
- entre com o valor de n
- tecle n
- tecle i
EXERCÍCIOS RESOLVIDOS
Nota: Se você possuir uma calculadora HP12C, use as sequências indicadas acima para resolver os problemas abaixo.
1 - Quanto teremos daqui a 12 meses se aplicarmos $ 1.000,00 a 2,5% ao mês?
Solução: FV = 1000(1 + 0,025)12 = $ 1.344,89
Notas:
a) é sempre conveniente, antes de operar com a HP 12C, teclar f CLEAR REG (limpa registradores), ou f CLEAR FIN (limpa registradores financeiros, mas, não limpa o visor).
b) para alterar o número de casa decimais apresentados pela calculadora HP
12C, estando ela ligada, tecle f seguido de um número 1, 2, 3, 4, ... etc., para obter no visor 1, 2, 3, 4 ... casas decimais. Por exemplo, o comando f 4, colocará a calculadora para exibir no visor 4 casas decimais.
c) na calculadora HP 12C, o termo registradores, significa memórias de armazenamento de dados, enquanto que o termo registradores financeiros, refere-se aos registros especiais nos quais são armazenados os valores de n, i, PV, PMT e FV.
2 - Quanto se deveria pagar hoje para se ter o direito de receber $ 10.000,00 daqui a 5 anos, a juros de 10% ao ano?
Solução: 10000 = PV(1 + 0,10)5\ PV = $ 6.209,21
3 - Calcular qual a taxa de juros a que devemos empregar o capital de $ 150.000,00 para render no final do período de 6 anos, o montante de $ 251.565,00?
Solução: 251565 = 150000(1 + i)6\ i = 9% a.a.
4 - O capital de $ 37.500,00 é colocado no regime de capitalização composta à taxa de 9% ao trimestre. No fim de um certo prazo, o montante atingiu $ 62.891,25. Calcular o número de meses.
Solução: 62891,25 = 37500(1 + 0,09)n\ n = 6 trimestres = 18 meses
Exercícios propostos
1 - Aplicando-se $ 1.000,00 por um prazo de dois anos a uma taxa de 5% ao semestre, qual será o montante no fim do período?
Resposta: $ 1.215,51
2 - Um capital de $ 2.000.000,00 é aplicado durante um ano e três meses à taxa de 2% a.m. Quais os juros gerados no período?
Resposta: $ 691.736,68
3 - Determinado capital aplicado a juros compostos durante 12 meses, rende uma quantia de juros igual ao valor aplicado. Qual a taxa mensal dessa aplicação?
Resposta: 5,94% a.m.
4 - Calcule o montante de $1000,00 aplicados a 10% a.a. durante 50 dias.
Resposta: $1013,89.