Sabemos de aula anterior, Teorema dos Senos que a área S de um triângulo ABC inscrito numa circunferência de raio R e cujos lados medem a, b e c é dada pela fórmula:
S = abc /4R
Sabemos também, da teoria exposta no mesmo arquivo anterior, que
c/senC = 2R (Teorema dos senos – TS).
Podemos então dizer que c = 2R.senC
Substituindo na fórmula da área acima, vem:
S = a.b.2R.senC / 4R , que simplificada fica:
S = (1/2).ab.senC , onde C é o ângulo formado pelos lados de medidas a e b .
Portanto, a área de um triângulo qualquer é igual ao semi-produto das medidas de dois lados pelo seno do angulo que eles formam entre si. Isto é o Teorema das áreas - TA.
Genericamente, podemos escrever a fórmula acima em função de qualquer par de medidas dos lados a saber:
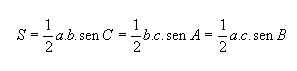
Exemplo : Dois lados de um triângulo medem 10cm e 20cm e formam entre si um angulo de 30º. Qual a área desse triângulo?
Solução: S = (1/2).10.20.sen30º = (1/2).10.20.(1/2) = 50cm2
Obs: sen30º = 0,5 = 1/2
Repetindo: a área de qualquer triângulo é igual a metade do produto de dois lados pelo seno do angulo que eles formam.