Força Centrífuga

Forças Inerciais

Todos os corpos próximos da superfície de um planeta como a Terra, por exemplo, independentemente de suas massas, apresentam a mesma aceleração devido à presença do campo gravitacional uniforme. O mesmo comportamento pode ser observado se for nula a resultante das forças que atuam sobre os corpos e o seu movimento for descrito em relação a um referencial não inercial. Como exemplo, consideremos um foguete no espaço interestelar, longe de qualquer outro corpo, com um astronauta e alguns objetos no seu interior. Com os motores desligados, foguete, astronauta e objetos se deslocam com a mesma velocidade em relação às estrela longínquas (Fig.a): o astronauta e os objetos flutuam no interior do foguete, em repouso em relação a ele. Agora, no instante em que os motores são ligados, o foguete passa a estar acelerado em relação às estrelas longínquas (Fig.b), onde a flecha representa o vetor aceleração).

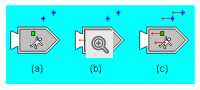Como o astronauta e os objetos ainda têm a mesma velocidade constante de antes, a plataforma traseira do foguete se aproxima deles com aquela aceleração. Assim, em relação ao foguete, isto é, em um referencial não inercial, o astronauta e os objetos se move em direção à plataforma traseira (Fig.c) com uma aceleração igual para todos, independentemente de suas massas, e de módulo igual ao módulo da aceleração do foguete em relação às estrelas longínquas. O astronauta e os objetos se movem como se estivessem em um campo gravitacional uniforme. Portanto, do ponto de vista de um observador não inercial, aparece um campo de forças equivalentes a um campo uniforme de gravidade. Essas forças, que não podem ser associadas às interações fundamentais e que surgem nos sistemas de referência acelerados (não inerciais), são chamadas de forças inerciais. Em sistemas de referência giratórios aparecem a força centrífuga e a força de Coriolis. Vamos discutir agora em detalhe a força centrífuga.

Referencial Inercial

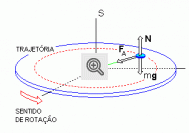Seja um disco na horizontal girando com velocidade angular constante e com uma moeda em repouso relativamente a ele. Tomando como referencial para descrever o movimento da moeda um referencial inercial como, por exemplo, aquele representado por S na, cuja origem coincide com o centro O do disco e com um de seus eixos cartesianos coincidindo com o eixo de rotação do disco, o movimento da moeda é um movimento circular uniforme (MCU). Então, a força resultante sobre a partícula é chamada força centrípeta e tem módulo FC = mv2/R onde m, v e R representam, respectivamente, a massa, o módulo da velocidade linear e o raio da trajetória circular da moeda.

Nesse referencial inercial atuam, sobre a moeda, três forças: a força peso (mg), vertical e apontando para baixo, a força normal (N), vertical e apontando para cima, e a força de atrito estático (FA), horizontal e apontando para o centro O da trajetória. A soma vetorial da força peso com a força normal é zero porque a moeda não tem movimento vertical. Assim, a força de atrito estático, que a superfície do disco exerce sobre a moeda, é a resultante das forças que atuam sobre a moeda e é, portanto, a força centrípeta que causa o movimento circular uniforme da moeda: FC = FA. Se se pudesse fazer desaparecer a força de atrito estático, a primeira lei de Newton garante que, a partir desse instante, o movimento da moeda seria um movimento retilíneo e uniforme (pelo menos enquanto estivesse sobre o disco). Assim, o movimento da moeda é circular e uniforme porque a força de atrito estático causa uma aceleração centrípeta de módulo constante.

No espírito da terceira lei de Newton, a força de reação à força peso da moeda, exercida pela Terra, é a força gravitacional que a moeda exerce sobre a Terra e que se pode imaginar atuando no centro da Terra, a força de reação à normal, que a superfície do disco exerce sobre a moeda, é a força que a moeda exerce sobre a superfície do disco no ponto onde se apóia e a força de reação à força (horizontal) de atrito estático que a superfície do disco exerce sobre a moeda é a força (horizontal) de atrito estático que a moeda exerce sobre a superfície do disco também no ponto onde se apóia.

Referencial Não Inercial

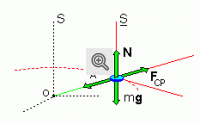Um referencial fixo na própria moeda como, por exemplo, aquele representado por S, é um referencial não inercial porque gira em relação ao referencial inercial S. Como a moeda está em repouso nesse referencial S, a resultante das forças que atuam sobre ela é zero. A força peso (mg), vertical e apontando para baixo, a força normal (N), vertical e apontando para cima, e a força de atrito estático (FA), horizontal e apontando para o eixo de rotação do disco, continuam agindo sobre a moeda e a soma vetorial da força peso com a força normal ainda é zero porque a moeda não tem movimento vertical. Mas a força de atrito estático não pode mais ser a resultante das forças que atuam sobre a moeda porque a moeda está em repouso nesse referencial S, de modo que a resultante de todas forças que atuam sobre ela deve ser zero. Assim, deve existir uma outra força atuando sobre a moeda, força essa que, somada vetorialmente com a força de atrito estático, deve dar uma resultante nula. Essa força, que só existe para um observador não inercial, e que tem o mesmo módulo e a mesma direção que a força de atrito estático, isto é, a direção da reta que passa pelo centro O do disco e pela moeda, mas sentido contrário, isto é, apontando do centro do disco para a moeda, é a assim chamada força centrífuga (FCF).

 A força de atrito estático entre duas superfícies em contato só existe se essas superfícies, embora em repouso relativo, tenham a tendência de se mover uma em relação à outra. Assim, a realidade da força centrífuga para o observador não inercial vem da tendência da moeda se mover em relação ao disco no sentido de se afastar do seu centro, tendência essa causada pela força centrífuga, e é por isso que aparece, simultaneamente, a força de atrito estático.

As forças que estamos chamando de forças inerciais porque não podem ser associadas às interações fundamentais e só aparecem nos sistemas de referência acelerados (não inerciais), são também chamadas de forças fictícias. Aqui, a palavra fictícias não deve induzir o pensamento de que elas são falsas ou ilusórias. Para o passageiro de um veículo que descreve uma curva, e que é jogado contra a lateral desse mesmo veículo pela força centrífuga, força essa que é tanto maior quanto maior a velocidade do veículo em relação à estrada e quanto menor o raio de curvatura da estrada, a força que a lateral do veículo exerce contra seu ombro, por exemplo, como reação à força que ele (o passageiro) exerce sobre essa lateral, é bastante real podendo, inclusive, causar desconforto local. Outra coisa é o fato de que essa força não existe sob o ponto de vista de um observador em um referencial inercial, que pode descrever o fenômeno pela propriedade de inércia do passageiro.

Já discutimos acima as forças de reação, no espírito da terceira lei de Newton, para as forças peso (mg), normal (N) e de atrito estático (FA). Para a força centrífuga não existe uma força de reação. Para um observador no referencial não inercial S, as forças centrífuga e de atrito estático têm módulos iguais, direções iguais e sentidos opostos, mas nem por isso constituem um par ação-reação porque atuam sobre o mesmo corpo e são de naturezas diferentes: a força de atrito estático é de caráter eletromagnético e a força centrífuga, um efeito devido ao caráter não inercial do referencial usado para descrever o movimento da moeda que não pode ser associado a qualquer interação fundamental.

Como se disse acima, a força centrífuga tem o mesmo módulo que a força de atrito estático, e como foi mostrado mais acima, a força centrípeta tem também o mesmo módulo que a força de atrito estático, de modo que a força centrípeta (vista pelo observador inercial) e a força centrífuga (vista pelo observador não inercial) têm o mesmo módulo.