O que é espaço?
O que é o espaço? Reconhecemos e usamos o espaço, mas se alguém perguntar o que é o espaço, muitos irão ter dificuldades em explicar. Na verdade, é mais fácil explicar o que se pode fazer com este ente primitivo que não tem definição para nós.
Uma primeira tentativa para explicar isto, é dizer que é tudo o que nos envolve e é o local onde podemos nos mover para a frente, para o lado e para cima.
Pelo conceito expresso, observamos que vivemos em um ambiente tridimensional. Basta então conhecer as três direções para identificar a posição relativa que ocupamos.
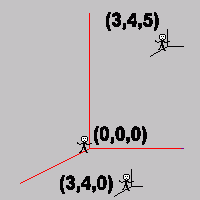
Quando afirmamos que vamos andar para a frente, para o lado e para cima, devemos quantificar e identificar o quanto iremos nos deslocar nestas direções, logo necessitamos conhecer uma origem para o sistema e identificar este ponto como (0,0,0) pois esperamos que ele esteja localizado a uma distância num ponto de referência para todos os outros pontos.
O Sistema Cartesiano tridimensional
Um procedimento matemático simples é tomar um ponto genérico como:
P=(x,y,z)
onde x indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para frente, y indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para o lado e z indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para cima.
Para facilitar as coisas do ponto de vista matemático, iremos denominar tais direções por: Eixo OX, Eixo OY e Eixo OZ.
O sistema tridimensional é o conjunto de todos os ternos ordenados (x,y,z), sendo que ordem não pode ser mudada sob pena de nos deslocarmos para outro lugar. A palavra cartesiano se deve a René Descartes, conhecido como cartesius. x recebe o nome de abscissa, y o nome de afastamento e z o nome de cota.
Exemplo: Se um indivíduo está no centro da cidade em uma posição O=(0,0,0) e quer andar para a frente 3 quadras, depois andar para o lado 5 quadras e depois subir até o 10o. andar de um prédio a posição final do mesmo após o percurso será o ponto P=(3,5,10) e podemos observar que as unidades não são necessariamente as mesmas. Se este mesmo indivíduo se deslocasse para a posição final P=(3,10,5), certamente chegaria a um lugar diferente.
Outros sistemas de localização
Existem outras formas de localização no espaço tridimensional como é o caso do sistema de coordenadas cilíndricas, sistema de coordenadas esféricas, dentre outros. Particularmente importantes são os sistemas de corrdenadas no plano. O sistema cartesiano plano é um caso particular do sistema cartesiano espacial tridimensional, mas existe um outro sistema muito importante que é o sistema de coordenadas polares.
O Sistema de Coordenadas Polares (R2)
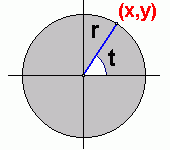
Vamos considerar agora um mundo plano onde os pontos são indicados por P=(x,y). No sistema bidimensional a medida x recebe o nome de abscissa e a medida y recebe o nome de ordenada.
Existe um sistema que considera uma linha básica horizontal de referência, por exemplo, o Eixo OX indicado positivamente e outra forma de indicar um ponto P=(x,y). Consideremos que a distância da origem O=(0,0) ao ponto P=(x,y) seja indicada por r e que o ângulo formado entre o segmento OP e o Eixo OX indicado positivamente seja indicado por t. Neste caso o ângulo deverá ser um parâmetro tal que 0<t<2Pi. Assim, um ponto será indicado por
P=(r,t)
onde
r = (x2+y2)½, e t = arctan(y/x)
Exemplo: Para um indivíduo pontual se deslocar da origem O=(0,0) ao ponto P=(3,4), ele deverá se deslocar 5 unidades na direção da reta que forma um ângulo de t=36.87 graus com o Eixo OX. Assim, o ponto será descrito como P=(3,4) ou em Coordenadas Polares como:
P=(5, 36.87)
A tangente de 36.87 graus = 0.75 = 3/4.
O Sistema de Coordenadas CilíndricasEste sistema considera duas linhas básicas que passam pela origem O=(0,0,0), uma linha de referência no plano do chão como o Eixo OX indicado positivamente, uma outra linha de referência como o Eixo OZ e o ângulo indicado por t e formado pela projeção no plano do chão do segmento OP e o Eixo OX indicado positivamente. O ângulo deverá ser um parâmetro tal que 0<t<2Pi. Assim, um ponto P=(x,y,z) será indicado por
P=(r,t,z)
Observamos que este sistema é uma mera ampliação das coordenadas polares, mantendo a mesma coordenada z, conhecida na literatura como a cota z.
A ideia básica para indicar um ponto neste sistema é construir um cilindro circular reto com o centro na origem 0=(0,0,0) e que passe exatamente pelo ponto P=(x,y,z). A projeção deste ponto no plano do chão que é indicada pelo plano z=0 é o ponto Po=(x,y,0) e determinamos as coordenadas polares do par ordenado (x,y) considerado como um ponto de um plano e não do espaço.
Exemplo: Para um indivíduo se deslocar da origem O=(0,0,0) ao ponto P=(3,4,10), ele deverá se deslocar 5 unidades na direção da reta que forma um ângulo de t=36.87 graus com o Eixo OX e subir 10 unidades, logo o ponto será descrito como P=(3,4,10) ou em coordenadas cilíndricas como:
P=(5, 36.87, 10)
O Sistema de Coordenadas Esféricas
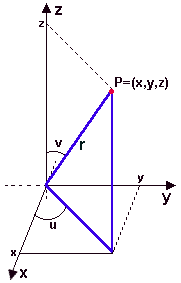
Este sistema considera o plano do chão (z=0) que passa pela origem O=(0,0,0) contendo o Eixo OX orientado positivamente e o Eixo OZ orientado positivamente, que é uma linha reta perpendicular ao plano do chão.
Neste sistema, o ponto P=(x,y,z) é indicado por três medidas: r a distância entre O=(0,0,0) e o ponto P=(x,y,z), u o ângulo formado entre projeção no plano do chão do segmento OP e o Eixo OX indicado positivamente e v o ângulo formado entre o segmento OP e o Eixo OZ indicado positivamente.
Enquanto o ângulo u pode ser tal que 0<u<2Pi pois a projeção de OP sobre o plano do chão pode dar uma volta completa, o ângulo v pertence ao intervalo 0<v<Pi, pois este ângulo chega a ser no máximo um ângulo raso.
Assim, um ponto P=(x,y,z) será indicado por
P=(r,u,v)
onde
r = (x2+y2+z2)½ , u = arctan(y/x) e v = arccos(z/r)
Um Sistema Geográfico
Há um Sistema Geográfico de identificação de posição na face da Terra que leva em consideração outros objetos como: meridianos e paralelos, para indicar a longitude e a latitude do ponto na superfície do globo terrestre. Como uma circunferência de círculo tem um arco com 360 graus, os cientistas dividiram 360 graus por 24 (horas) para obter 15 graus por hora.
Consideraram a planificação do globo terrestre traçaram linhas imaginárias geodésicas (verticais) sobre a superfície terrestre, as quais passam pelos polos Norte e Sul e estas são denominadas meridianos e a referência básica foi a cidade de Greenwich (Inglaterra) que tem o meridiano 0.
Fizeram o mesmo com linhas horizontais na planificação e denominaram tais linhas de paralelos. Hoje podemos observar a localização de uma cidade em qualquer lugar do mundo situada no meridiano M e paralelo P. E´ lógico que cada local está localizado com a cota z acima do nível do mar, razão pela qual este sistema pode ser indicado como:
P=(M,P,z)
Exemplo: O Terminal Rodoviário da cidade XYZ está localizada na posição (a,b,c). Resolva este problema para a sua cidade.
O Sistema cartesiano R4
Você já pensou que ao invés de estar num sistema tridimensional como dissemos antes, talvez você esteja num sistema tetradimensional? Na verdade, vivemos num sistema R4, pois são necessárias 4 coordenadas para indicar a posição relativa de um objeto.
Um objeto colocado às 12:00 h no ponto (3,4,12) não é o mesmo objeto colocado às 13:00 h no mesmo ponto (3,4,12).
Para entender melhor, exija um sacrifício de uma pessoa e a coloque parada (se possível, estática) às 12:00 h em um local de sua casa, que tomaremos como o ponto (3,4,12). Você espera que esta pessoa seja a mesma pessoa às 13:00 h? É óbvio que aconteceram modificações no comportamento da mesma, mesmo que você não tenha observado.
Você acha que uma árvore plantada em um local por mais de 20 anos é a mesma a cada instante? O corpo humano também é composto de átomos que se movem a uma velocidade que não pode ser visualizada, assim, um corpo está em constante movimento e dependendo dos estímulos recebidos das mais diversas fontes, terá alteração, logo não será o mesmo de antes, nem mesmo 1 segundo depois!
Até o momento já observamos como é possível estender o conceito de espaço a algo além daquilo que possamos desenhar ou conceber geometricamente.
Uma ideia sobre o Rn
Quando o governo calcula a inflação de um determinado período, ele afirma que a inflação inf é uma função que depende de várias variáveis como X(xuxu), A(abacate), Co(Condomínio), Ca(Carro), E(Escola), I(Indecisão do governo), D(Dívida Interna), E(etc) e outros "objetos". Uma pessoa normal colocaria o Xuxu ou limão como um dos itens para a análise e cálculo da inflação?
Isto significa a um matemático sério, que
inf = f(X,A,Co,Ca,E,I,D,E)
e é logico que esta função é bem construída e é consistente, no entanto você não consegue desenhar o gráfico da mesma nesse ambiente tridimensional que você vive. Isto indica que você está trabalhando em um sistema com as 8 coordenadas (X,A,Co,Ca,E,I,D,E), logo o gráfico desta função deve estar em R9. Para obter seriamente a inflação você precisa medir o comportamento de n (ou centenas de) variáveis e não somente de poucas.
Isto não quer dizer que a inflação é uma função construída para enganar o povo. Na verdade, o que deveria ser feito para obter a inflação é a consideração das principais variáveis que causam esta alteração no Sistema Financeiro Nacional, mas uma coisa é óbvia: O governo não leva em consideração os fatores que realmente distorcem o processo inflacionário pois não considera nesses cálculos os fatores que geram tal inflação mas somente alguns elementos da cesta básica que nada tem a ver com a realidade nacional.
Com este exemplo, eu espero ter dado uma ideia sobre o significado do espaço Rn, que é uma mera extensão dos espaços bidimensional e tridimensional, nossos velhos conhecidos.
A nossa capacidade ainda é muito pequena para entender um espaço multidimensional Rn.
Observemos a passagem bíblica citada no início deste trabalho, que nos diz que existem outros ambientes (espaços) que o senso de um homem comum é incapaz de conceber.
Ha uma necessidade do ser humano alterar o seu comportamento para ver algo além das coisas comuns desse mundo. Há muitas pessoas que olham para uma parede de uma casa e não conseguem ver nada além dela. Você já se imaginou num quarto de uma casa, pensando exatamente que estivesse no quarto vizinho com todas as coisas boas ou ruins que o mesmo possui? Será que você é daqueles que percorre o trajeto de sua casa até o seu serviço sempre usando o mesmo caminho? Você já pensou que na outra rua existem (coisas ruins e) coisas belas que você nunca percebeu porque nunca passou por lá?